Grad shape
Grad shape

Web Browser History

Get started
hero image
    🙏

    জয়  শ্রী  রাম

     🕉




Problem Statement:


You have a browser of one tab where you start on the homepage and you can visit another url, get back in the history number of steps or move forward in the history number of steps.

Implement the BrowserHistory as follows:

BrowserHistory(string homepage) Initializes the object with the homepage of the browser.

void visit(string url) Visits url from the current page. It clears up all the forward history.

string back(int steps) Move steps back in history. If you can only return x steps in the history and steps > x, you will return only x steps. Return the current url after moving back in history at most steps.

string forward(int steps) Move steps forward in history. If you can only forward x steps in the history and steps > x, you will forward only x steps. Return the current url after forwarding in history at most steps.

Example:
BrowserHistory browserHistory = new BrowserHistory("example.com");
browserHistory.visit("google.com"); // You are in "example.com". Visit "google.com"

browserHistory.visit("facebook.com"); // You are in "google.com". Visit "facebook.com"

browserHistory.visit("youtube.com"); // You are in "facebook.com". Visit "youtube.com"

browserHistory.back(1); // You are in "youtube.com", move back to "facebook.com" return "facebook.com"

browserHistory.back(1); // You are in "facebook.com", move back to "google.com" return "google.com"

browserHistory.forward(1); // You are in "google.com", move forward to "facebook.com" return "facebook.com"

browserHistory.visit("linkedin.com"); // You are in "facebook.com". Visit "linkedin.com"

browserHistory.forward(2); // You are in "linkedin.com", you cannot move forward any steps.

browserHistory.back(2); // You are in "linkedin.com", move back two steps to "facebook.com" then to "google.com". return "google.com"

browserHistory.back(7); // You are in "google.com", you can move back only one step to "example.com". return "example.com"

Solution:

While solving this design problem I would show you how to methodically go from O(n) approach to O(1) approach using your critical thinking ability and clear understanding of data structures. Please pay special attention to how we systematically optimize our solution. This is one of the qualities we are trying to build in you in this course and would greatly help you in your interviews as well as later in your software engineering career to stand out and get promoted and progress towards becoming an architect.


O(n) Doubly LinkedList based O(n) Approach and its drawbacks:


This solution is based on a very simple thought process: take a linkedlist to store the visited webpages in sequence (in the order they are visited). We have the older visited webpages towards the tail, and the more recently visited webpages towards the head. Since we have both forward() and back() methods, that means that we need to move on both sides of the linkedlist, this means that we would need a doubly linkedlist. This approach would automatically come to your mind if you have gone through LRU Cache and LFU Cache.

The simple code below implements the above algorithm:

Java Code:

// Implementation using Doubly LinkedList
class BrowserHistory {
    
    Node head; // most recently visited webpage
    Node tail; // webpage visited longest ago
    Node current; // webpage we are currently at
    
    public BrowserHistory(String homepage) {
        // when the first webpage is visited
        // that webpage becomes head, tail and current
        // becuase we have only one webpage as of now
        head = new Node(homepage);
        tail = head;
        current = head;
    }
    
    public void visit(String url) {
        Node newNode = new Node(url);
        
        // Requiremnets for visit(string url) method: Visits url from the current page. It clears up all the forward history.
        
        newNode.next = current; // the webpage to which current node currently points to goes one step back in history from the currently 
        // visited webpage which means the webpage which current node is pointing to becomes next node of the currently visited webpage
        current.prev = newNode; // the newly visited node becomes previous node of the webpage that is currently being pointed to by the current node
        
        head = newNode;  // newly visited webpage becomes head. This clears all forward history
        current = head; // newly visited webpage becomes current webpsge
    }
    
    public String forward(int steps) {
        // Requirements for forward(int steps) method: Move steps forward in history. 
        // If you can only forward x steps in the history and steps > x, 
        // you will forward only x steps. Return the current url after forwarding in history at most steps.
        
        Node node = current;
        // go towards head
        while (node.prev != null && steps > 0) {
            node = node.prev;
            steps--;
        }
        current = node;
        return node.url;
    }
    
    public String back(int steps) {
        // Requirements of back(int steps) method: Move steps back in history. 
        // If you can only return x steps in the history and steps > x, you will return only x steps. 
        // Return the current url after moving back in history at most steps.
        
        Node node = current;
        // go towards tail
        while (node.next != null && steps > 0) {
            node = node.next;
            steps--;
        }
        current = node;
        return node.url;
    }
    
    class Node {
        public String url;
        public Node prev;
        public Node next;
        
        public Node(String url) {
            this.url = url;
        }
    }
}


Python Code:

class BrowserHistory:
    def __init__(self, homepage):

        self.head = Node(self, homepage)
        self.tail = self.head
        self.current = self.head

    def visit(self, url):
        newNode = Node(self, url)
        newNode.next = self.current
        self.current.prev = newNode
        self.head = newNode
        self.current = self.head

    def forward(self, steps):
        node = self.current
        while node.prev is not None and steps > 0:
            node = node.prev
            steps -= 1
        self.current = node
        return node.url

    def back(self, steps):
        node = self.current
        while node.next is not None and steps > 0:
            node = node.next
            steps -= 1
        self.current = node
        return node.url


class Node:

    def __init__(self, outerInstance, url):
        self.url = None
        self.prev = None
        self.next = None

        self._outerInstance = outerInstance

        self.url = url


Drawback:
This doubly linkedlist based approach is not a good approach to be implemented in a language which does not have support in-built garbage collection due to the risk of data leak that would arise when we are clearing the forward history and re-assigning the head. The webpages which are cleared from the forward history should be handled by the developer to make sure there is no data leak if the above approach is implemented in a language like C++ where there is no garbage collection.


Time Complexity: O(n)
Space Complexity: O(n)

O(n) Approach using Two Stacks:


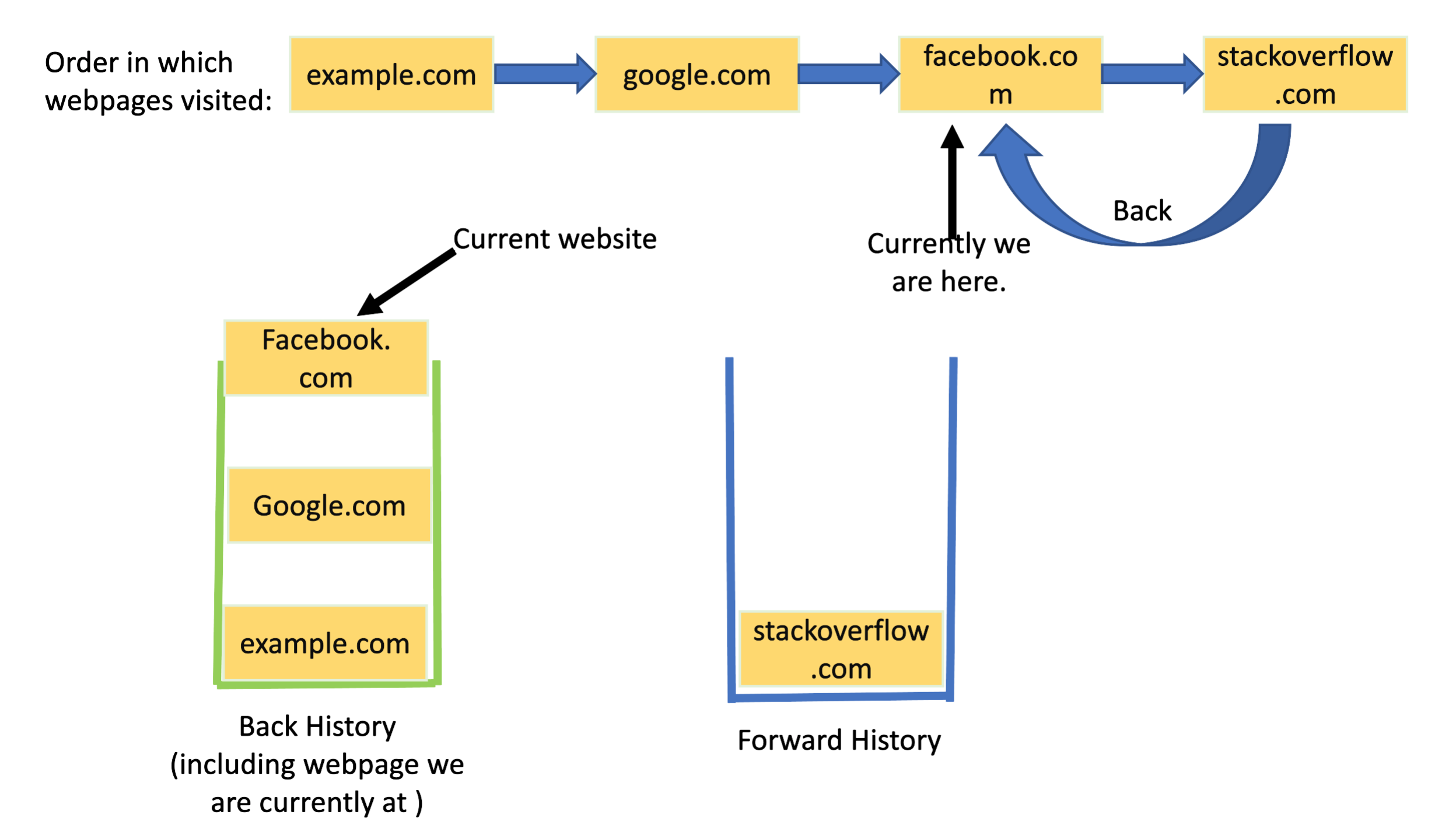
This approach is one of the simplest and intuitive and a perfect use of stack data structure. You keep two stacks:
  • Stack for storing back history: Lower the position of a webpage in the stack, the older it is in history.
  • Stack to store forward history: Lower the position of a webpage in the stack, the more forward in the history it is.
Now what about the current webpage ? You can keep the current webpage on top of either one of the two stacks. For the solution below, I choose to keep it on top of back history stack.

The picture below beautifully illustrates the concept introduces above.

Look at the simple code below and everything we discussed so far would become crystal clear:
Code:

Java: 


// Two Stacks Approach
class BrowserHistory {
    
    Deque<String> backHistory; // stack to contain current webpage and all its back pages, which means webpage on top of this stack is the current webpage we are at
    Deque<String> forwardHistory; // stack to store all forward webpages of the current webpage we are at
    

    public BrowserHistory(String homepage) {
        backHistory = new ArrayDeque<>();
        forwardHistory = new ArrayDeque<>();
        backHistory.push(homepage);
    }
    
    public void visit(String url) {
        backHistory.push(url);  
        forwardHistory.clear(); // clear all forward history
    }
    
    public String back(int steps) {
        while (!backHistory.isEmpty() && steps > 0) {
            forwardHistory.push(backHistory.pop());
            steps--;
        }
        if (backHistory.isEmpty()) {
            backHistory.push(forwardHistory.pop());
        }
        return backHistory.peek();
    }
    
    public String forward(int steps) {
        while (!forwardHistory.isEmpty() && steps > 0) {
            backHistory.push(forwardHistory.pop());
            steps--;
        }
        return backHistory.peek();
    }
}

Python: 


import collections


class BrowserHistory:
    def __init__(self, homepage):

        self.backHistory = None
        self.forwardHistory = None

        self.backHistory = collections.deque([])
        self.forwardHistory = collections.deque([])
        self.backHistory.insert(len(self.backHistory), homepage)

    def visit(self, url):
        self.backHistory.insert(len(self.backHistory), url)
        self.forwardHistory.clear()

    def back(self, steps):
        while (not len(self.backHistory) == 0) and steps > 0:
            self.forwardHistory.insert(len(self.backHistory), self.backHistory.pop())
            steps -= 1
        if len(self.backHistory) == 0:
            self.backHistory.insert(len(self.backHistory), self.forwardHistory.pop())
        return self.backHistory.index(0)

    def forward(self, steps):
        while (not len(self.forwardHistory) == 0) and steps > 0:
            self.backHistory.insert(len(self.backHistory), self.forwardHistory.pop())
            steps -= 1
        return self.backHistory.index(0)


Time Complexity: O(n)
Space Complexity: O(n)

O(n) solution using One List :

Instead of keeping two data structures, can we just use one ? Yes we can, we just need to keep track of the index of the current webpage at all time. Please see the code below:
Java Code:

class BrowserHistory {
    
    List<String> visitedWebpages;
    int currentIndex;

    public BrowserHistory(String homepage) {
        visitedWebpages = new ArrayList<String>();
        visitedWebpages.add(homepage);
        currentIndex = 0;
    }
    
    public void visit(String url) { // O(n)
       currentIndex++;
        // do not do visitedWebpages.add(currentIndex, url), instead do as shown below: it optimizes complexity from O(n) to O(1)
        if (currentIndex <= visitedWebpages.size() - 1) {
            // update
            visitedWebpages.set(currentIndex, url); // replace. This optimizes time complexity rather than doing add(index, value) operation since add(index, value) is O(n) but set() is O(1)
        }
        else {
           // add at the end of the list
           visitedWebpages.add(url); // O(1)
        }
       visitedWebpages.subList(currentIndex + 1, visitedWebpages.size()).clear(); // clear all forward history // clear() is O(n) operation
    }
    
    public String back(int steps) { // O(1)
        currentIndex = Math.max(0, currentIndex - steps);
        return visitedWebpages.get(currentIndex); // O(1)
    }
    
    public String forward(int steps) { // O(1)
        currentIndex = Math.min(visitedWebpages.size() - 1, currentIndex + steps);
        return visitedWebpages.get(currentIndex); // O(1)
    }
}
The above implementation is not O(1) because in visitedWebpages.subList(currentIndex + 1, visitedWebpages.size()).clear(); // clear all forward history code clear() is O(n).

Python Code:

import math


class BrowserHistory:
    def __init__(self, homepage):
        self.visitedWebpages = []
        self.visitedWebpages.append(homepage)
        self.currentIndex = 0

    def visit(self, url):
        self.currentIndex += 1
        if self.currentIndex <= len(self.visitedWebpages) - 1:
            self.visitedWebpages[self.currentIndex] = url
        else:
            self.visitedWebpages.append(url)
        self.visitedWebpages[self.currentIndex + 1: len(self.visitedWebpages)].clear()

    def back(self, steps):
        self.currentIndex = max(0, self.currentIndex - steps)
        return self.visitedWebpages[self.currentIndex]

    def forward(self, steps):
        self.currentIndex = min(len(self.visitedWebpages) - 1, self.currentIndex + steps)
        return self.visitedWebpages[self.currentIndex]


Time Complexity: O(n)
Space Complexity: O(n)

O(1) time complexity solution with O(n) space trade-off:

Look how the clear() method in visit() method is the root cause of the time complexity to be O(n) and not O(1). One of the requirements is when we call visit() it should erase all forward history. If we want to remove the forward history from our data structure it would be O(n) no matter how much optimization we do. But it saves space since we are deleting the forward history from the data structure altogether.
So if we really want to optimize space we would have to do a trade-off on space. What if we do not delete the forward history, instead keep where the current foward history ends ? This optimizes the space complexity to O(1) but at a cost of huge space requirements. No wonder, why some web browsers are memory hog!!

The below code implements this O(1) algorithm:

Java code:


// O (1) solution using one list
class BrowserHistory {
    
    List<String> visitedWebpages;
    int currentIndex;
    int currentHistorySize; // to keep track of where the forward current history end

    public BrowserHistory(String homepage) {
        visitedWebpages = new ArrayList<String>();
        visitedWebpages.add(homepage);
        currentIndex = 0;
        currentHistorySize = 1;
    }
    
    public void visit(String url) {
        currentIndex++;
        if (currentIndex <= visitedWebpages.size() - 1) {
            visitedWebpages.set(currentIndex, url); // replace. This optimizes time complexity rather than doing add() operation since add(index, value) is O(n) but set() is O(1)
        }
        else {
           visitedWebpages.add(currentIndex, url); // O(1)
        }
        currentHistorySize = currentIndex + 1;
    }
    
    public String back(int steps) {
        currentIndex = Math.max(0, currentIndex - steps);
        return visitedWebpages.get(currentIndex);
    }
    
    public String forward(int steps) {
        currentIndex = Math.min(currentHistorySize - 1, currentIndex + steps);
        return visitedWebpages.get(currentIndex);
    }
}


Python code:


class BrowserHistory:
    def __init__(self, homepage):
        self.visitedWebpages = []
        self.visitedWebpages.append(homepage)
        self.currentIndex = 0
        self.currentHistorySize = 1


    def visit(self, url):
        self.currentIndex += 1
        if self.currentIndex <= len(self.visitedWebpages) - 1:
            self.visitedWebpages[self.currentIndex] = url
        else:
            self.visitedWebpages.insert(self.currentIndex, url)
        self.currentHistorySize = self.currentIndex + 1

    def back(self, steps):
        self.currentIndex = max(0, self.currentIndex - steps)
        return self.visitedWebpages[self.currentIndex]

    def forward(self, steps):
        self.currentIndex = min(self.currentHistorySize - 1, self.currentIndex + steps)
        return self.visitedWebpages[self.currentIndex]


Time Complexity: O(1)
Space Complexity: O(n)

Instructor:

Abhishek Dey

Abhishek Dey

Senior SDE | Chief Architect

AWS | Microsoft | University of Florida

View LinkedIn profile